Chemcept-data has been designed for rapid estimation of physical and chemical properties from limited source data. It is available as object code for customers to build into their own programs or (against a confidentiality agreement) as C++ source code. The following properties are computed:

Liquids:

Mixture Density (as function of Temperature)
Mixture Viscosity (as function of Temperature)
Mixture Specific Heat at Constant Pressure (assumed constant)
Mixture Heat of Combustion (assumed constant)

Gases:

Mixture Density (as function of T and P).
Mixture Z-value and first Virial Coefficient (as functions of T and P)
Mixture Viscosity (as function of T and P)
Mixture Heat Capacity (as a function of Temperature and Pressure)
Mixture Heat Capacity Ratio (as a function of T and P).
Mixture Lower Flammable Limit (assumed constant)
Mixture Heat of Combustion ("low" non-condensed water value, assumed constant)
Mixture Stoichiometric Oxygen requirement for combustion.
Mixture Enthalpy (as a function of Temperature and Pressure)
Note that the enthalpy is thermodynamically consistent with the heat capacity and the equation of state.
Mixture Thermal Conductivity (to be added 2005).

Vapour-liquid equilibria.

This facility will not be released until late 2004. It takes advantage of a strong correlation between Heat Capacity at low pressure and temperature, and the acentric factor.

Summary of Methods and data used.

The equations are based on reduced property correlations. The correlations enable values to be estimated based on very little data. Users can also easily find, or estimate, the required data for additional species. The data required are:

Molecular Weight
Critical Temperature, Pressure and Volume
Heat Capacity at Constant Pressure at STP
Heat of Combustion at STP ("low" value for non-condensed water vapour)
Lower Flammable Limit
Stoichiometric Oxygen required for combustion.

The database has about 50 compounds built in. The database is an ASCII file (plain text file) that is easily extended by the user.

The estimation system is designed to be integrated with the programs using the methods. The system is written in ISO C++ so that, in principle, it can be used on any computer and operating system with an ISO-compliant C++ compiler. There are significant benefits in direct access to properties through functions rather than accessing them through middleware (the method employed by CAPE-OPEN). Thus, the program writer knows exactly the form of the equations used and the valid range over which they can be employed. The equations can be integrated with end-user programs allowing analytical, or simplified numerical, solutions to be employed instead of iterative methods and numerical integrations. Furthermore, algorithms can include conditional tests to ensure that the properties routines never "blow up", and that sensible results are returned for non-sensible conditions such as extremely high pressures or temperatures. Additionally, valid bounds can be returned to calling programs. Consequently, programs using the methods can be up to 10000 times faster and reliability is greatly improved. Both these characteristics are important in optimization, process synthesis and in design under uncertainty. Automatic optimization methods frequently generate intermediate values that are non-feasible or are orders of magnitude away from optimum. Conventional simulators fail under such circumstances; they are designed to be started with reasonable estimates and they do not solve if starting values are wildly wrong. Chemcept-data loses some of the CAPE-OPEN flexibility to swap estimation methods. However, alternative methods can be employed by adjusting the data values such that the simplified correlations match "rigorous" values exactly. With such an approach, the speed and reliability of the Chemcept methods can be married to the flexibility of CAPE-OPEN.

The feasibility and efficiency of this two-level approach has been demonstrated by Johns and Vadhwana in papers published in Trans I Chem E. Even for relatively simple "rigorous" properties, speed gains of over 1000 were achieved. Optimal refitting for a dual-level simulation gave the identical result to the "rigorous" system in 1/20 of the time. Since the work was published, the rigorous systems supplied by the major software companies have become slower and more complex. The Chemcept systems have become faster and simpler. Thus, we would now expect much greater speed gains than we have previously achieved. The Chemcept approach to simulation and optimization is to provide very fast, very robust simulation/design capability. This increase in performance is achieved at some cost in precision. In this respect, our products are entirely complementary to those offered by the major simulator suppliers (such as AspenTech). We certainly do not compete with physical properties specialists such as Infochem UK Ltd. Our systems can get close to an optimal answer very quickly and reliably. The accuracy of their systems is probably in excess of an order-of-magnitude better. Thus, we provide a rapid optimization/synthesis and case-study capability while the systems offered by the major suppliers are needed to verify operability and to fine-tune the optimization. At the same time, our systems are directly applicable where lower precision is inevitable. For example, the properties that we estimate enable pressure drops to be computed within a fraction of a percent of the "rigorous" results. The underlying friction-factor correlations are less accurate than 10%. In these circumstances, the Chemcept System needs no further refining.

The program employs a pressure virial equation for the gas phase. The benefits of this equation are that it is explicit in both pressure and volume, and that the temperature correlation is simple. Thus, most common thermodynamic relationships can be solved analytically both for differentiation and integration.

We summarize the methods and their accuracy as follows:

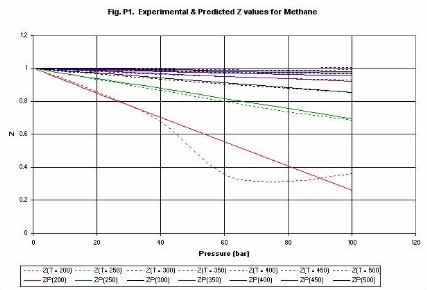Compressibility factor (Z). Figures P1 (methane) and P2 (ethylene) give examples of the estimation of values of the compressibility factor Z. The lines are identified as follows, Z(300) is compressibility at 300 K, ZP(300) is the compressibility predicted by the Chemcept Pressure Virial Equation of State.

The critical properties of methane are (Pc = 45.9 bar, Tc = 190.6 K), and for ethylene are (Pc = 50.3 bar, Tc = 282.3 K). Thus, typically at above the critical temperature errors are less than 2%. The equation is not designed to be used in the near-critical region. Thus, the methane line for 200 K, shows deviations above about 40 bar. However, it behaves sensibly through the critical region.

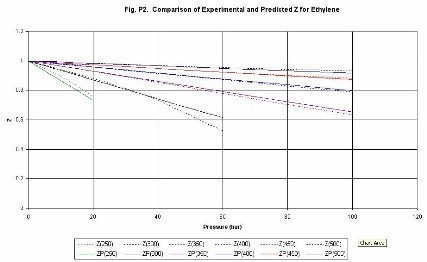Thus, optimizations for which the final result is non-critical work well. The iteration through the critical region is easier and more reliable than iterations employing equations of state that are accurate in the region.

Figure P3 compares experimental and estimated Heat Capacities for Methane. The correlation employed only uses one measured Cp value. The temperature and pressure correction is derived from the reduced equation of state. It is seen that the data are correlated with simple straight lines over a wide range of conditions. Most physical-properties data systems employ complex correlations that are difficult to manipulate other than numerically. Other systems ignore the dependence of heat capacity on pressure. For example, they typically employ the ideal-gas approximation that Cp = Cv + R. Chemcept-data does not make this ideal-gas approximation, although it applies asymptotically at low pressures and high temperatures. Furthermore, Chemcept-data allows for the variation of Heat Capacity Ratio with temperature and pressure, which can be important in near sonic flow of high-pressure gases. Thus, Chemcept-data allows reliable computation in regions where some more sophisticated systems show shortcomings.

Vapour Viscosity is computed using the well-known relationships of Stiel & Thodos, corrected for high pressures by the equation of Dean & Stiel. These equations are claimed to be accurate to 3% at low pressures and up to 5% at high pressures. The mixing rules quoted in the Chemical Engineer's Handbook are incorrect, and improved mixing rules are employed in Chemcept-data. For turbulent flow calculations, viscosity is typically raised to the 0.25 power, so that errors of less than 1% can be expected. Typical errors in turbulent flow pressure-drop and heat transfer equations exceed 10%, so that the error resulting from physical property estimation is negligible.

Liquid Density is computed using a variant of the Rackett equation with our own mixing rules. An error of less than 5% is expected. Water is often an exception to these general estimation methods. For liquid properties, we have decreased the critical volume of water by 5% in order to obtain accurate density estimates.

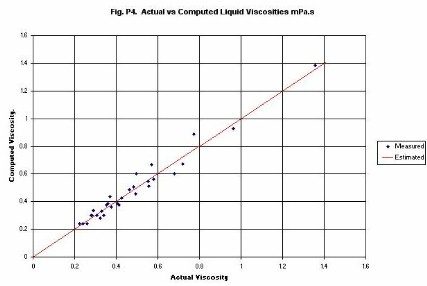Liquid Viscosity is computed from an original equation. The equation uses kinetic theory to estimate the energy term in the temperature dependence formula. Thus, the activation energy is a constant multiplied by RTc. Computed viscosities for a range of compounds are given in Figure P4.

The compounds included are: Water, p-Xylene, Octane, Nonane and Dodecane (all in the range 298 K to 373 K).

Benzene and Toluene (range 298 K to 348 K), and Hexane (range 298 K to 323 K).

Note that, without any special treatment, the viscosity of water is well predicted.

In the next web-site update, we will present the VLE methods employed.